The project Caesars granted by the Agence Nationale de la Recherche for years 2016-2018 aims at fullfiling four primary tasks, that is

task 1. development of efficient algorithms for stochastic control based on BSDEs;

task 2. advances in stochastic games and mean-field games;

task 3. rare event estimation in concerning risk management;

task 4. quantification of uncertainty on models and their parameters;

A few examples concerning electrical systems that involve developements of the above tasks are:

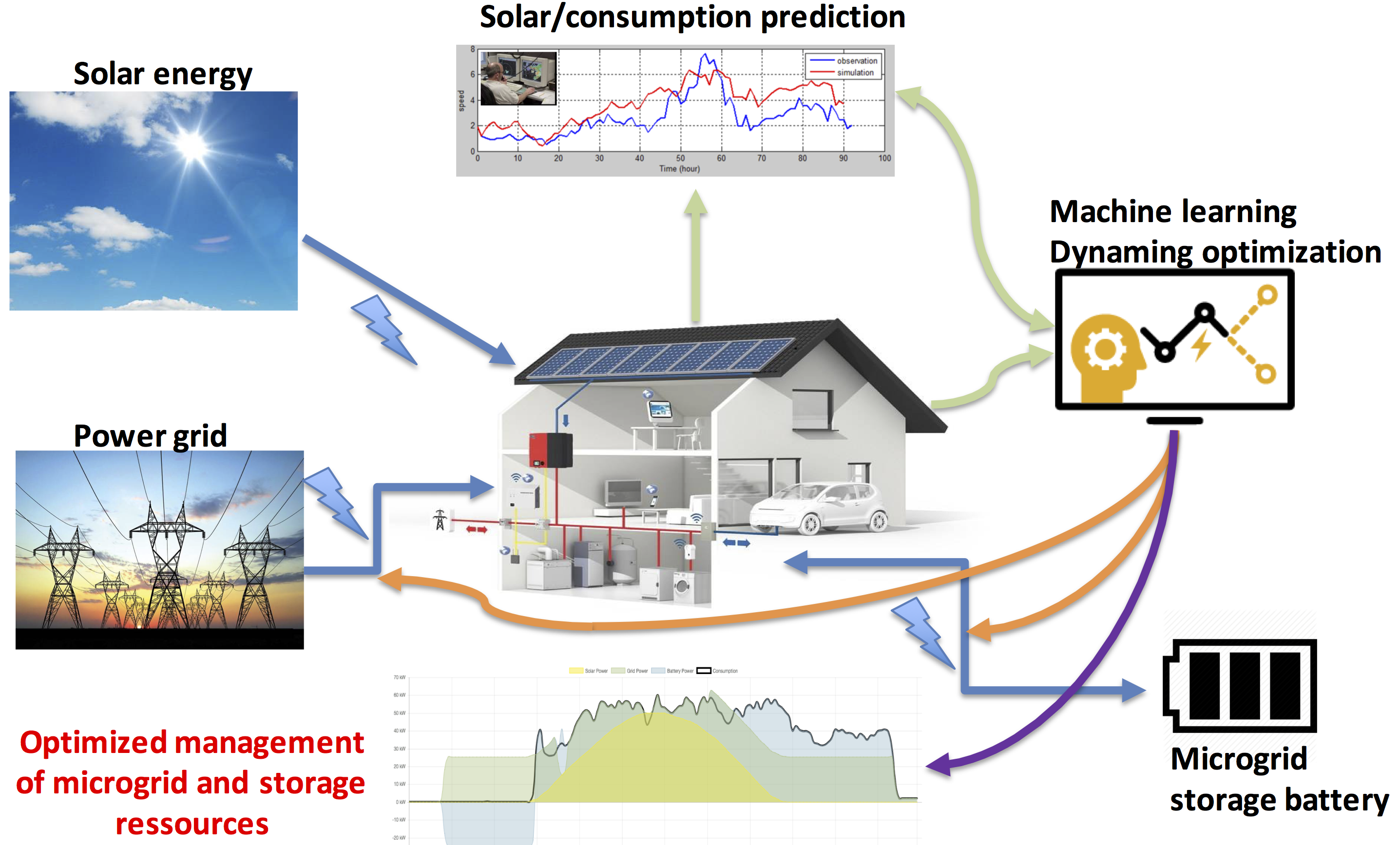
• Optimal management under uncertainty of microgrid equipped with PV panels and battery: We describe the mathematical modeling and the numerical resolution of the optimal management of the electricity consumption of a building equipped with solar panels and battery. The storage facilities help to smooth the load on the public grid. We address the question of how to use optimally the battery in order to minimize the variance of power taken from the public grid. We also account for the aging of the battery by penalizing in our optimisation criterion the charge/discharge of the battery. We additionally expect that the State Of Charge of the battery remains close to a medium value. This is a new type of stochastic control problem since we need to account for the probability distribution of the system (here the variance). We have tackled this problem by designing and solving a new type of stochastic equation called McKean Forward Backward Stochastic Differential Equations. Joint work by Emmanuel Gobet and Maxime Grangereau.

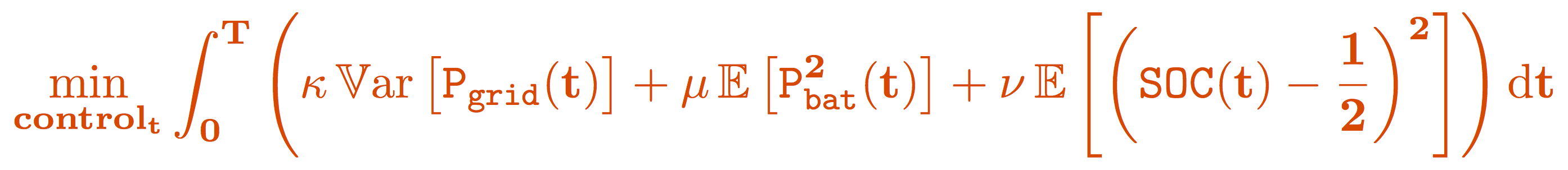
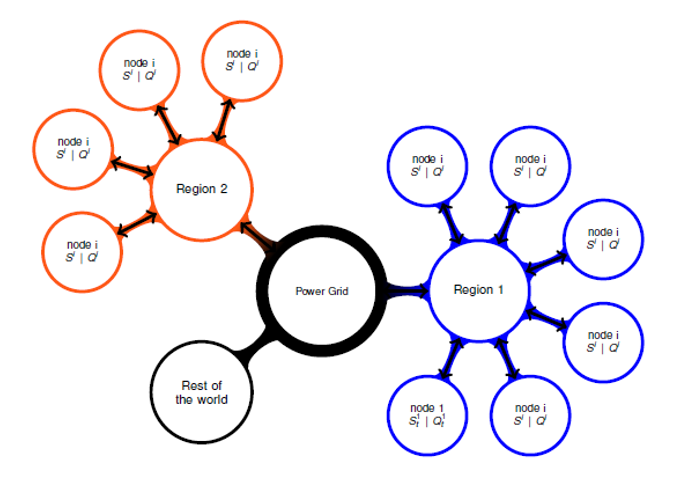
• Grid With Distributed generation and storage: We consider a stylized model for a power system with distributed local energy generation and storage. This system is modeled as a grid connecting a large number of nodes, where each node is characterized by a local electricity consumption, has a local electricity production (e.g. photovoltaic panels), and manages a local storage device. Depending on its instantaneous consumption and production rates as well as its storage management decision, each node may either buy or sell electricity, impacting the electricity spot price. The objective at each node is to minimize energy and storage costs by optimally controlling the storage device. In a non-cooperative game setting, we are led to the analysis of a non-zero sum stochastic game with $N$ players where the interaction takes place through the spot price mechanism. For an infinite number of agents, our model corresponds to an Extended Mean-Field Game (EMFG). In a linear quadratic setting, we obtain and explicit solution to the EMFG, we show that it provides an approximate Nash-equilibrium for $N$-player game, and we are able to compare this solution to the optimal strategy of a central planner.